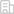生態系統中環境與生物變量之間壓力-響應關系是生態學各領域研究探索的一個基本理論問題,也是支撐各類環境現實問題管理有關標準制定和評估決策的關鍵科學依據。例如,水體環境中營養鹽與葉綠素之間的關系,一直是生態學,特別是淡水生態學與數理統計學跨學科研究中一個典型的“找關系”理論問題,已成為水體富營養化定量評估和營養物基準制定等方法體系建設的重要生態學基礎。從生態學基本定義出發,在生態系統尺度上準確定量環境與生物變量之間壓力-響應關系,一方面對促進相關學科交叉前沿研究具有理論意義,另一方面對環境現實問題的科學管理具有實踐應用價值。
在生態系統研究中,環境與生物變量關系的不穩定性不僅困擾著理論生態學界甚至引起一些有趣但可能不必要的爭論,同時也制約著這類關系在環境現實問題管理中的應用。鑒于此,城市環境研究所科研人員聯合賓夕法尼亞州立大學、日本國立環境研究所等單位研究同行,以營養鹽與葉綠素之間關系為例提出生態變量關系“時間不穩定性”或“時域依賴性(Temporal dependence)”的概念性假設,同時構建了檢驗該假設的統計學路徑(圖1)。這一概念性假設和檢驗路徑及案例解析以題名為“A statistical framework to track temporal dependence of chlorophyll–nutrient relationships with implications for lake eutrophication management”正式發表在《Journal of Hydrology》。
這一概念性假設的基本內涵包括相互聯系的兩個層面,一是營養鹽與葉綠素之間關系可能會因為觀測數據的時間不同而表現出不穩定,二是這一關系可能會隨著觀測數據時間樣本數量的不斷增加而逐漸趨于穩定。針對上述兩個層面,科研人員構建的統計學路徑由兩個相對應的檢驗流程組成,第一個流程用于檢驗單年樣本數據集生態變量關系的上邊界參數是否隨時間不同而變異,第二個流程用于檢驗逐年累積樣本數據集生態變量關系的上邊界參數是否隨時域增加而收斂。詳細的檢驗流程可參見上述已發表的論文。
這一概念性假設得到了來自美國和日本兩個不同案例湖泊長期觀測數據的一致性檢驗。檢驗的結果表明,兩個不同案例湖泊營養鹽與葉綠素上邊界單年模型參數均呈現出頻繁的波動,而逐年累積模型參數均呈現趨穩的趨勢。這一結果在湖泊富營養化管理和決策上意味著:“這兩個不同案例湖泊的水體富營養化評估和營養物基準制定,應基于逐年累積數據的趨穩化模型,而不應基于單年數據的波動性模型”。值得注意的是,盡管這一概念性假設得到兩個不同案例湖泊長期觀測數據的一致性檢驗,并對這兩個湖泊本身管理具有一定的啟示意義,但是這項研究仍然無法斷定該假設在全球湖泊中具有普適性。對此,這一概念性假設及其檢驗路徑的應用依然需更多具體案例湖泊長期觀測數據的檢驗。
這一概念性假設的檢驗路徑與主要科研人員多年前的兩項研究工作在統計學基本方法上“一脈相承”。這些研究工作統計學基本方法均采用分位數回歸(Quantile Regression, QR)。分位數回歸有別于最小二乘法線性回歸以“均值”作為擬合的對象,或者說是后者以“最大值”即上或下邊界作為擬合對象,已逐漸成為定量解析“李比西最小因子限制定律”的一個主流統計學方法。該方法創建于計量經濟學變量關系研究,并逐漸發展和應用于數量生態學領域。據悉,主要科研人員多年前將方法用于湖泊富營養化定量評估路徑的更新,并以營養鹽與葉綠素關系為例構建了總氮和總磷雙自變量相對重要性的檢驗路徑。